关于量子退火算法的一些了解
本人并非量子力学相关专业人士,本文是在我搜集资料和个人理解的基础上整理出来的,仅供参考。
量子退火算法(Quantum annealing,QA)是一种基于量子特性的量子计算机算法,由经典计算机上的模拟退火算法(又称经典退火算法)演化而来。
有的人认为量子退火算法可能是目前为止最重要的量子算法,并且量子退火算法已经在超级计算机上被模拟过了。
而人类第一台商用量子计算机 D-Wave 就是一种只能运行量子退火算法的专用量子计算机,Google 和 NASA 合建的量子人工智能实验室用的就是这种计算机。
本文将会沿着【为什么需要引入量子退火算法 ➡️ 量子退火算法的简单原理和优势 ➡️ 量子退火算法的应用和前景】的思路,整理一下我这几天对量子退火算法的一些了解。
经典计算机处理问题遇到的困难
由于算力和算法等方面的限制,经典计算机无法很好地解决某些问题,比如组合优化问题。
组合优化问题
先说最优化问题。最优化问题是寻找一个目标函数的极大极小值。大多数机器学习问题最后都会转化为一个最优化问题。最优化问题一般分成两类:一类是连续变量的问题,另一类是离散变量的问题。具有离散变量的问题,就称为组合优化问题。
组合优化问题一般是从一个无限集或者可数无限集里寻找一个对象,比如一个整数,一个集合,一个排列,或者一个图。即组合优化问题的解一般是一个离散空间。
旅行商问题(Travelling salesman problem, TSP)是一个经典的组合优化问题:给定一系列城市和每对城市之间的距离,求解访问每一座城市一次并回到起始城市的最短回路。
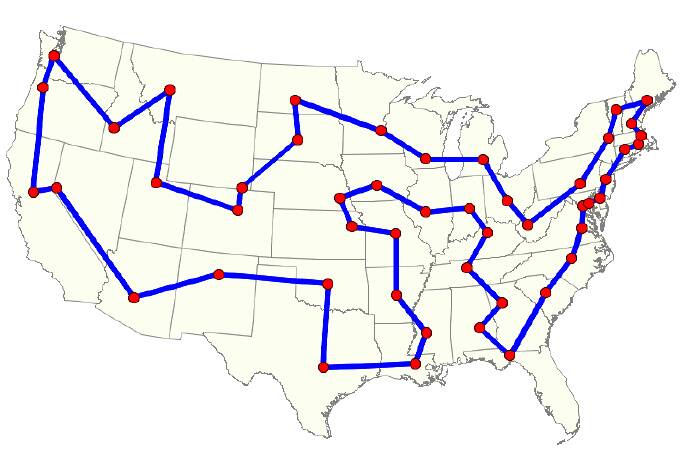
旅行商问题是一个 NP-Hard 问题,其算法复杂度为 。如果 较大,则经典计算机将很难解决这样的问题。
引入模拟退火算法
为了更好地解决组合优化问题,科学家们发明了模拟退火算法。
在冶金学中,退火是将材料加热后再经特定速率冷却,目的是增大晶粒的体积,并且减少晶格中的缺陷。材料中的原子原来会停留在使内能有局部最小值的位置,加热使能量变大,原子会离开原来位置,而随机在其他位置中移动。退火冷却时速度较慢,使得原子有较多可能可以找到内能比原先更低的位置。
模拟退火算法的基本原理:
- 以搜寻空间内一个任意点作起始点,以该点的状态作为临时最优解
- 按照一个预设的概率选择一个近邻点
- 计算该近邻点所代表的解与临时最优解相比是否为更优解。如果是更优解则更替该紧邻点的解为临时最优解,反之则临时最优解不变
- 循环步骤 3 和 步骤 4
- 足够多次的循环后,临时最优解会依概率收敛到全局最优解
可以看出,模拟退火算法的原理和金属退火的原理十分相似:模拟退火步骤 2 中提到的预设的概率和金属退火时加热的温度很像。通过这个预设的概率,临时解可以离开原来的位置,尝试发现更优解:
- 金属退火中,在一定限度内,加热温度越高,原子能够移动的距离越远,最后局部内能比原先更低的可能性越大。
- 模拟退火中,在一定限度内,预设概率越大,临时解能够找到的点越多,最后临时解是全局最优解的可能性越大。
值得强调的一点是,在两种退火中,预设一个概率和控制加热的温度都是一种扰动。在该扰动下,解空间尝试不断发生改变,来发现并筛选出更优的解空间,最后一定概率会收敛到最优解空间。按照我的理解,这就是退火算法的核心思想。这甚至让我联想到了生物进化论。
这里请先尝试理解模拟退火,后文中会提到模拟退火算法的具体例子以便加深理解。
量子退火的优越性
虽然对于许多组合优化问题,模拟退火算法已经有了不错的效果,但是对于某些问题,模拟算法要获得更优解会很费劲,需要大量的算力和时间。而量子退火算法可以更好的(甚至是碾压式地)解决这些问题。接下来先介绍一下粒子的波函数与量子隧穿效应,再从理论和实例两个维度来说明量子退火算法的优越性。
粒子的波函数与量子隧穿效应
这里说的波函数与某些说法中的物质波或德布罗意波,可能是指同一种东西。本文为了严谨,一律使用波函数这个称呼。
前文说过,按我的理解,加入扰动来发现更优解是退火算法的核心思想。那么控制粒子的波函数(即改变粒子的哈密顿量)就是量子退火算法的扰动。
在量子尺度,微观的物理对象都具有波动性和粒子性,其位置、动量、能量等在经典物理中确定的量都是不确定的。一个粒子有可能同时坐着飞机和高铁从杭州到达北京,这是经典物理无法解释的现象。而粒子的波函数和量子隧穿效应就是量子力学中粒子具有波动性的表现。
在量子力学里,量子隧穿效应指电子等微观粒子能够穿入或穿越位势垒的量子行为,尽管位势垒的高度大于粒子的总能量。
降维举例来说,这就像是墙边的一个人在一定概率下可以出现在墙的另一边(和瞬移有本质区别)。在经典力学里,这是不可能发生的。
实际上,在量子力学中,粒子什么时候出现在哪里是一个概率问题。这个概率可以通过该粒子的波函数来反映。

如图,蓝色部分即表示该粒子的波函数。该粒子的波函数可以辐射到容器外,即该粒子有一定概率可以出现在容器外。
从理论的角度说明量子退火的优越性
在模拟退火计算收敛的过程中,经常会遇到一些非常高但很薄的势垒,如下图所示:
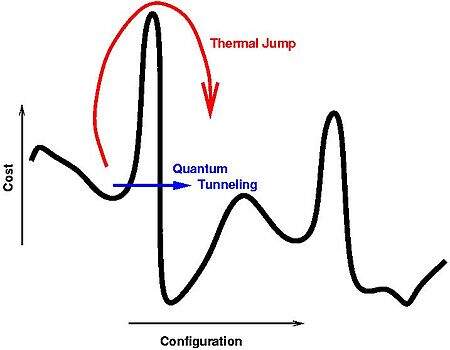
对于模拟退火算法,只能像图中的红色箭头一样,需要增大概率(即增加温度,增加能量),来使其到达山顶,之后有需要花大量的时间来收敛(即降温)。
而对于量子退火算法,就有一定的概率可以像图中的蓝色箭头一样,直接出现在势垒的另一边。
这种情况下量子退火相比模拟退火具有明显的优越性。
从实例的角度说明量子退火的优越性
这里使用爬山算法(贪心算法的一种)的例子来说明。
爬山算法指的是以以一个任意值为起始点,计算临近的解,然后不断判断这个解和符合条件的差距,选择选择更适合的方向继续计算,直到达到一个任意方向都是更劣解的位置。
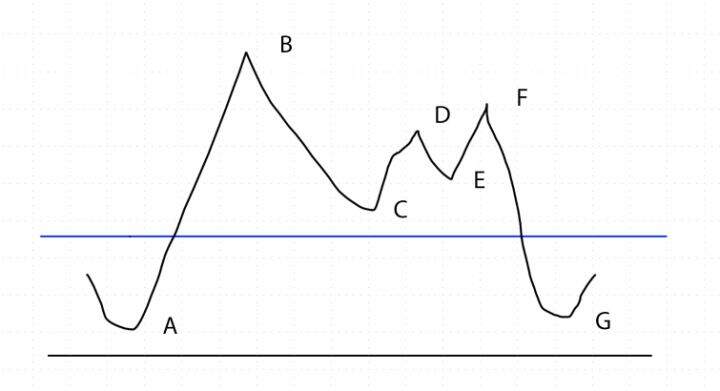
假设图中蓝线的位置就是要求的解,初始点产生在 DE 段。
如果采用模拟退火算法,从初始点的左右近邻点来看,E 点是局部最优解。想要获得比 E 更优的解,就必须增大扰动,扩大近邻点的范围。但想从 E 点爬出来并找到更优解依然是一个不容易的过程。特别是假如好不容易找到了更优解 C,则要找到全局最优解就变得难上加难。
而如果采用量子退火算法,效果如下所示:
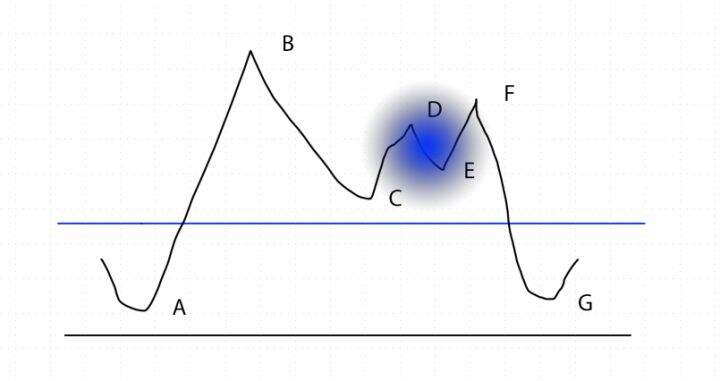
此时这位攀登者并不是处于 DE 的某一点,而是其波函数所辐射的这一片区域。这位攀登者有一定概率直接出现在 CD 并找到更优解 C,也有一定几率能出现在 FG 上并找到全局最优解之一。同时,因为量子的叠加性质,量子计算元件可以同时处在图中的很多个位置。这样以来,搜索的效率可以以 2 的指数倍增长。
这种情况下量子退火相比模拟退火具有明显的优越性。
实现量子退火
量子退火算法已经在经典计算机上模拟过了,也生产出了能运行量子退火算法的 D-Wave 量子退火机。
在经典计算机上模拟
量子退火算法在经典计算机上模拟主要使用蒙特卡罗方法。
蒙特卡罗方法(Monte Carlo method),也称统计模拟方法,是一种使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。
物理上实现量子退火机
通过蒙特卡罗方法模拟量子退火是非常低效的。研究人员认为其只有在量子计算机上才能表现出优势。
量子比特
量子退火机上的量子比特实际上是一个超导环,如下图左所示。其上有电流流动。电流流动带来磁效应,自旋向上(逻辑态 1)和自旋向下(逻辑态 -1),由电流顺逆流动来决定。磁悬可以被设计成量子力学的叠加态,所以可以作为量子比特。
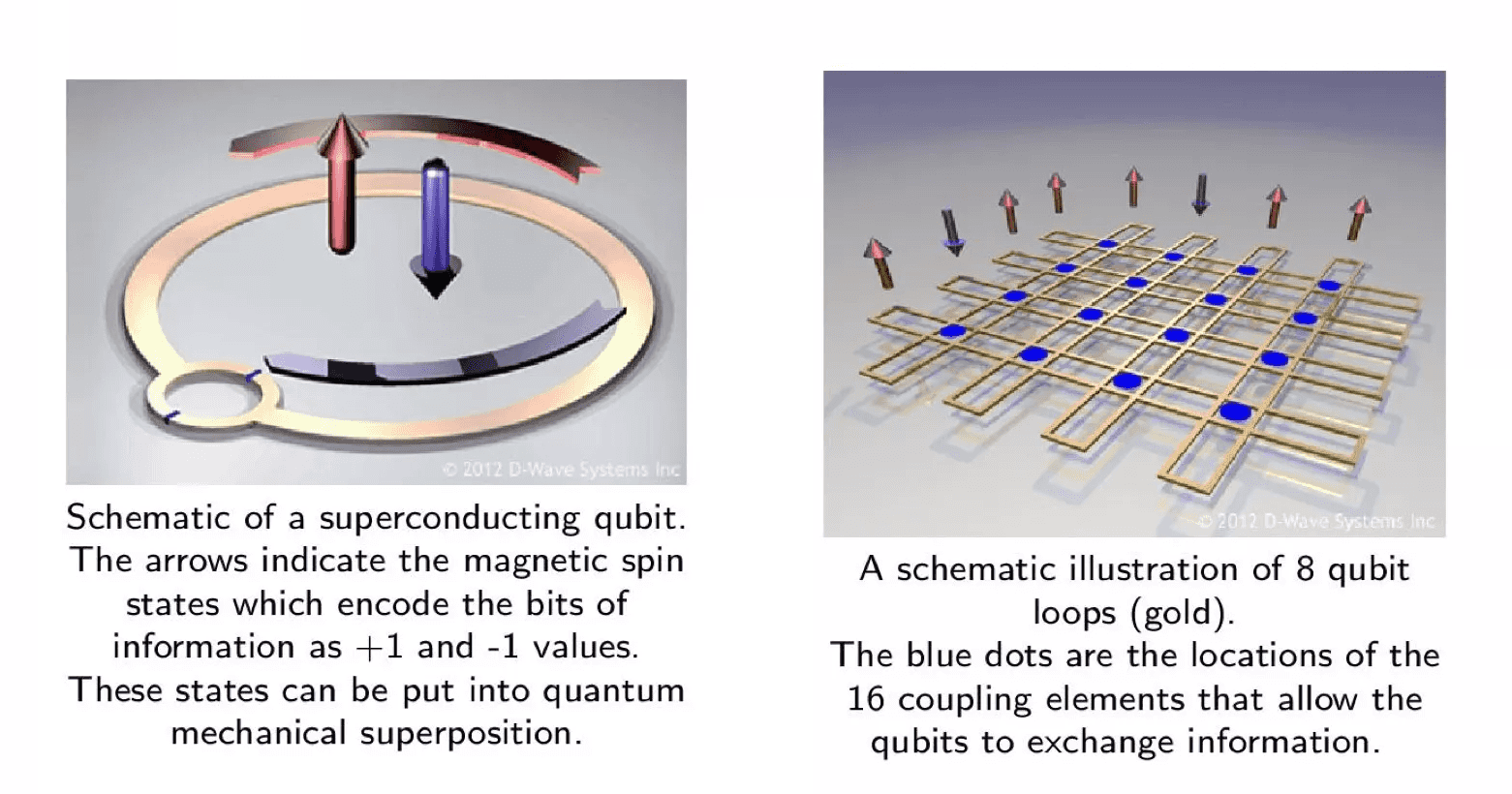
实际上的量子比特如上图右所示,每两个线圈的交点都是一个量子比特,8 个通电线圈组成了 16 个量子比特。
D-Wave
由于 D-Wave 量子计算机只能用来运行量子退火算法,业界对于这种非通用性的计算机是否属于量子计算机仍有争议。所以把 D-Wave 计算机成为量子退火机可能更为合适。

量子退火机上的量子退火处理器:
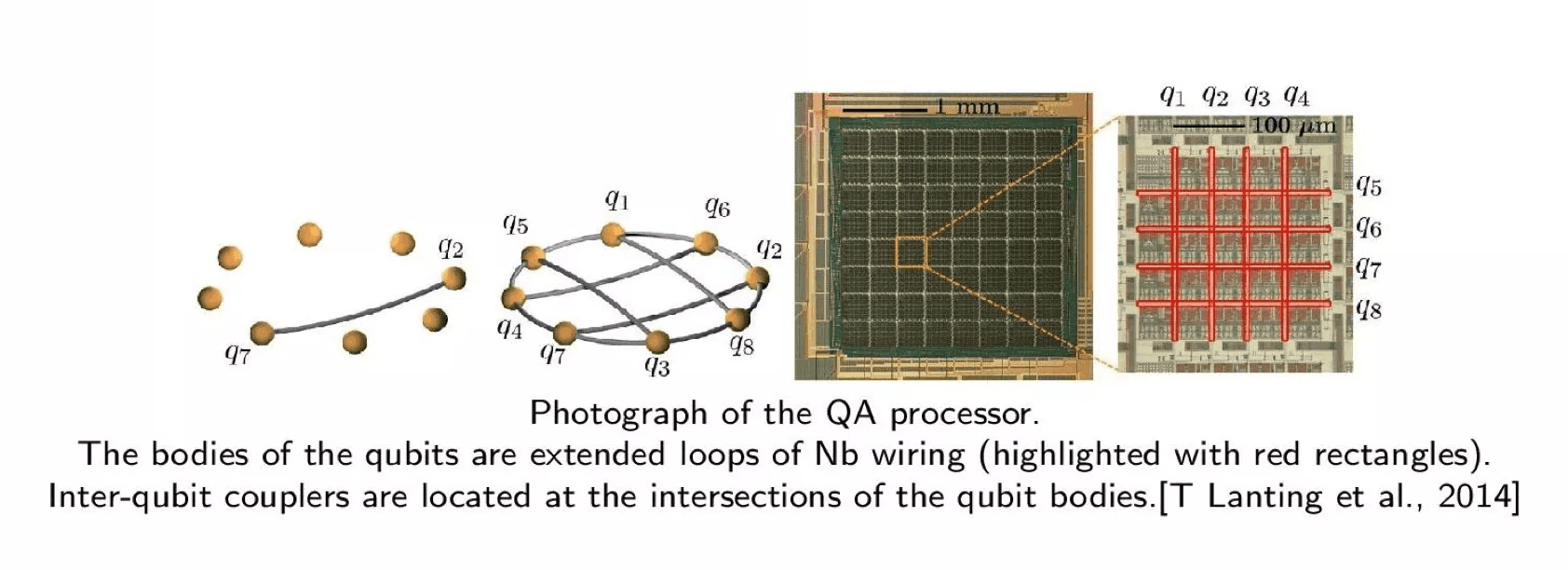
实际应用
量子退火机已经被尝试性地用于某些领域,比如:
- 自来水管道优化问题,用来避免水压局部过高过低,降低管道整体费用等
- 用来研究怎么降低放射性疗法对人体的损害
- NASA 用来优化星际旅行路径
关于两个重要争论
科学家们围绕量子退火机有两个比较重要的争论。
是不是真正在利用量子效应在做计算
2014 年,Google 的一个实验室做了一个实验,使用 D-Wave 量子退火机来求解寻找伊辛模型的基态问题。
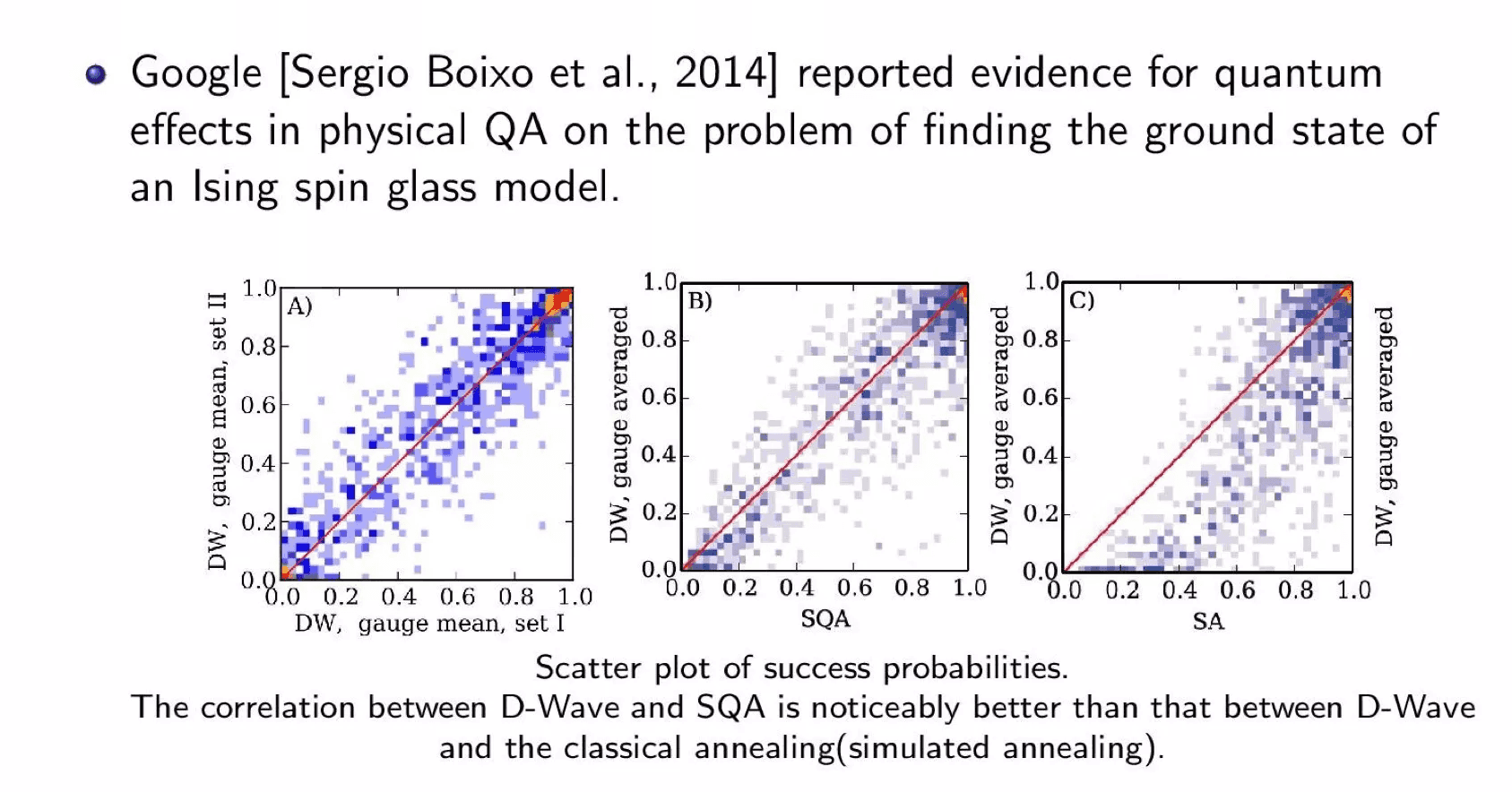
实验发现,D-Wave 量子退火机的行为模式和模拟量子退火的行为模式高度接近,拟合程度很高。而和模拟退火相比,差别非常远,拟合程度很低。所以 Google 该团队认为量子退火机是真正在利用量子效应在做计算的。
量子退火机上的量子退火有没有实现量子优势
量子霸权(Quantum Supremacy),或称量子优越性,是指用量子计算机解决经典电脑实际上解决不了的问题,问题本身未必需要有实际应用。
量子优势(Quantum Advantage)则是指量子电脑在解决实务问题上能比经典电脑更快而带来的优势,从计算复杂性理论的角度来说,这通常代表量子电脑相对最佳经典算法的加速是超多项式的。
2016 年,Google 另一个实验室做了一个实验,同样是一个寻找基态的问题。但是这个问题有点特殊,其能量情况比较复杂,尤其适合使用量子退火算法来解决。
如下图所示,Google 对比了 D-Wave 量子退火机和蒙特卡罗方法模拟量子退火,发现量子退火机的量子退火实现了量子优势。
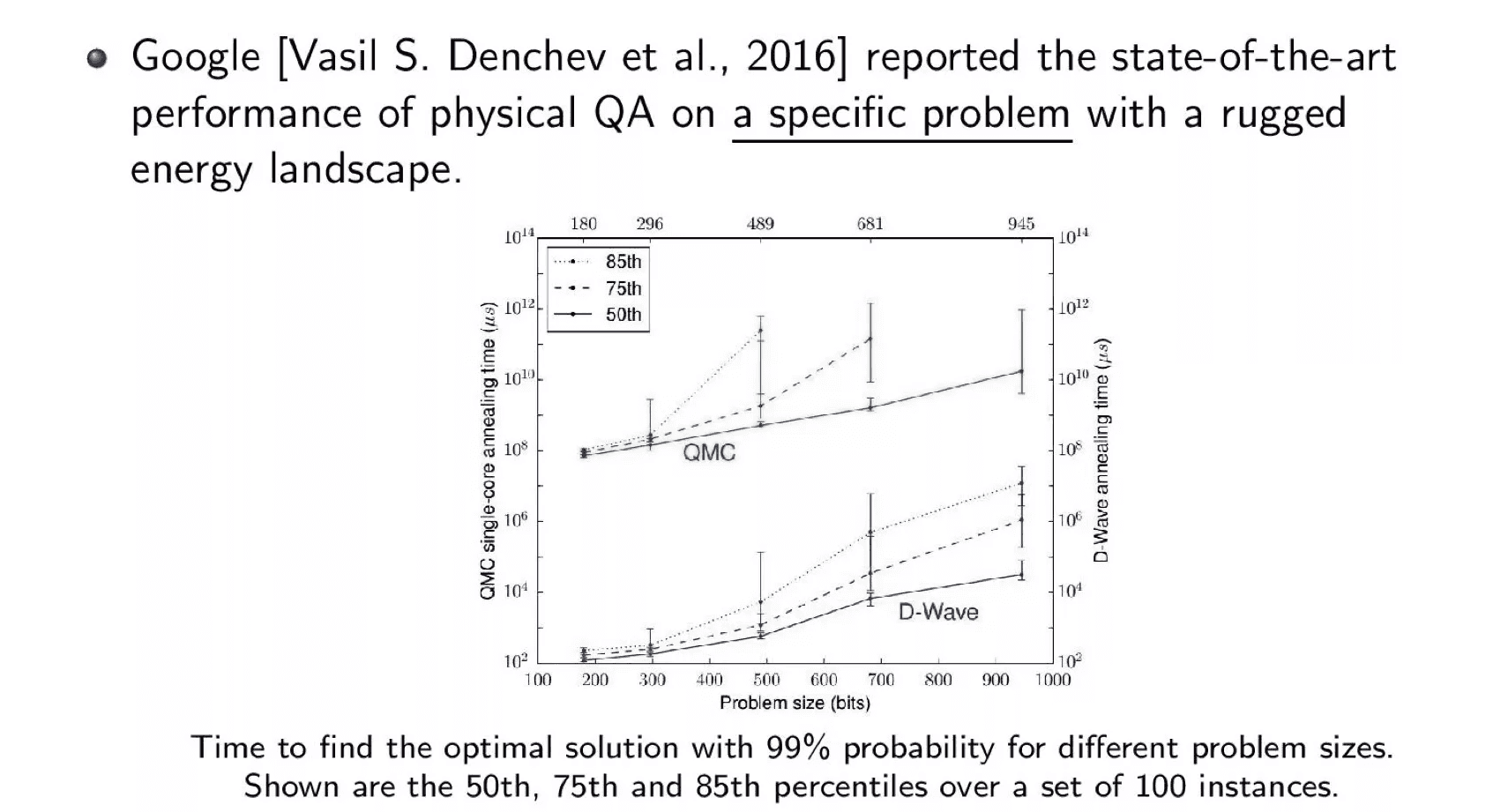
比如,对于 945 个变量的情况,1000 个量子比特的量子退火机的性能是运行在单核处理器上的模拟量子退火算法性能的 倍。
不过有科学家提出质疑:
- 认为量子退火机应该和经典超级计算机相比,而不是和一台单核计算机相比
- 认为 Google 不能只拿适合量子退火解决的问题来实验,也应该尝试一些更普遍的问题来验证量子优势
- 对于很多经典的组合优化问题,已经有了不少的经典优化算法,量子退火机和这些优化后的经典算法相比效果如何
2019 年,Google 宣称量子霸权已经实现:在世界第一超算 Summit 需要计算 1 万年的实验中,谷歌的量子退火机只用了 3 分 20 秒。
这在知乎引发了许多讨论:知乎:如何评价 Google 宣称率先实现量子霸权
总结
本文沿着【为什么需要引入量子退火算法 ➡️ 量子退火算法的简单原理和优势 ➡️ 量子退火算法的物理实现】的思路,整理一下我这几天对量子退火算法的一些了解。
总的来说,近几年在 Google 等的大力推动下,量子退火机实现了飞速的发展,并且已于去年宣布实现了量子霸权。但是量子退火只能用于解决某些特定问题,除非能研究出具有量子优势的通用型量子计算机,否则专用型的量子计算机还是很难影响经典计算机的地位。
参考: